With the growth of 24h distribution application developed by Chappiebot Inc., we are in need of an algorithm to test many models with the same purpose to see whether which one is the best. The traditional method is A/B Test. However, it is observed that this old-fashioned way becomes inefficient in this Big Data age. In this blog, I will discuss some alternative methods to it.
I. A/B Testing
Before diving into alternative approaches, we will present some primary points about A/B test. In A/B test, we compare two distinct models to check which one is superior. A group of user A continues using the old model, while the other group (B) experiences the new one. After a while, based on the statistics, we will have the winner-takes-it-all scheme: If the old one wins, everything stays where it is, nothing will be changed. Or else, the new model will be rolled out into production for every user.
This method is very popular in software development. For instance, sometimes the friend next to you shows you some functionality of the Facebook app but you don’t have even though you two use the same version.
Pros and cons
-
As we can see, this method is super intuitive and simple to implement. Although it is based on a statistical model, people with no stats background are still able to comprehend it easily.
-
From some perspectives, it is inefficient. We have to to wait a while to have the winner model and have to stick with this model for a long time even though maybe at some point in the future, it isn’t the best anymore. It is not optimal, we aim to find a data-driven solution: we can change the solution over time.
-
Moreover, when the stats between the options differs slightly, it is difficult to choose the winner.
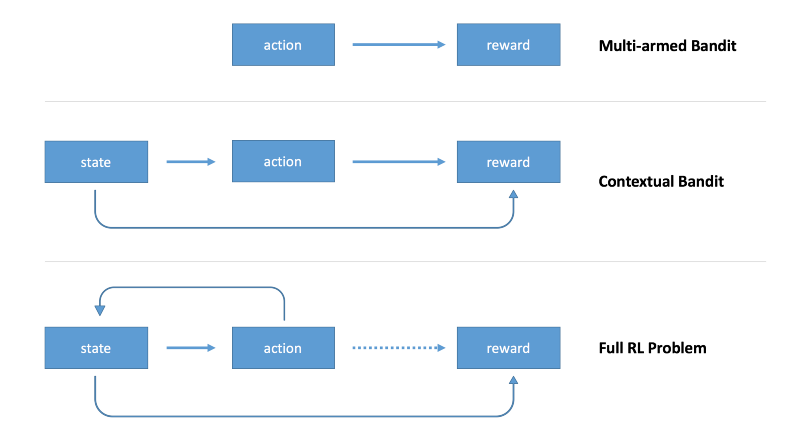
II. Multi-Armed Bandits (MAB)
Based on the previous observation, some brightest minds in Data Science look for the alternative to revise the testing. And in this process, Multi-Armed Bandits shows some potentials.
The name comes from the One-Armed Bandits machines in the casino. This machine has a lever for you to try your luck to win the reward (in fact, it is tuned to lighten your pocket).

Imagine you enter a room with many slot machines like that. The strategy to win must be finding which machine to play, in which order to play. Our objective is to maximize the reward through a sequence of lever pull. Multi-Armed Bandits method basically is composed of:
-
Exploration phase: You will spare equally all the machine a fraction of your times.
-
Exploitation phase: You will stick to the machine with the best stats obtained from the exploration phase.
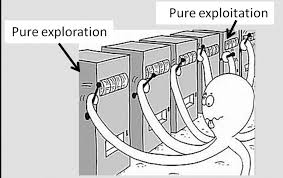
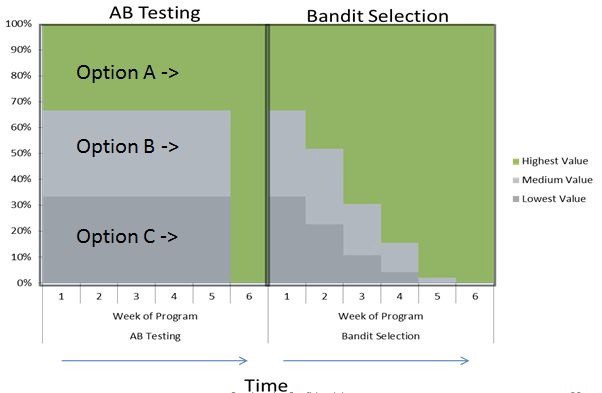
A/B will solve this problems by dividing the money into 2 accounts. First it will use the first account to try all the machines to see which one is the best, then it will stick with that machine till the end with the other account. As comparison, A/B testing employs a short exploration phase and long exploitation phase. They are sequential: one after the other.
Personally, it is not so complicated. Now all the leftover is finding the strategy to determine the exploration and exploitation rate. There are three methods here:
- Epsilon-Greedy: the rates for each one are fixed.
- Upper Confidence Bound: the rates are dynamically updated with respect to the UCB of each arm.
- Thompson Sampling: the rates are adjusted with respect to the entire probability distribution of each arm.
Epsilon-Greedy is by far the most popular for its simplicity and efficiency.
Pseudo-code for Epsilon-Greedy:
def choose():
if math.random() < 0.1:
# exploration
# choose randomly 10% of the time
else:
# exploitation
# for each lever
# calculate the reward expectation
# choose the lever with the largest reward expectation
# increment the number of times the lever has been played
def reward(choice, amount):
# save the reward to the total for the given lever
III. Example
Imagine we are testing the color for the button Share. There are 3 options: Green, Blue, Red. At the beginning, we initialize the value for each color is 1/1=100%. This number is chosen arbitrarily: it doesn’t matter what we choose, it will adapt itself for the task.
| Green | Blue | Red |
|---|---|---|
| 1/1 | 1/1 | 1/1 |
Firstly, we choose the one with highest probability (exploitation phase). Since it is all the same, we display randomly the Green. But the user says No:
| Green | Blue | Red |
|---|---|---|
| 1/2 | 1/1 | 1/1 |
Successively, the following ones say no to the Blue and the Red:
| Green | Blue | Red |
|---|---|---|
| 1/2 | 1/2 | 1/2 |
Suddenly, the fourth user prefer the Blue:
| Green | Blue | Red |
|---|---|---|
| 1/2 | 2/3 | 1/2 |
Till this point, the Blue button will have the higher chance to be display until its expected reward is lower than the others
| Green | Blue | Red |
|---|---|---|
| 115/5412 | 305/8700 | 166/2074 |
Randomization
We often see the 1/9 rate in Greedy-Epsilon method. Is it optimal?
The rate of the exploration and exploitation reflects the trade-off between trying some things new or sticking with the one working. A/B test spends 100% of its time to explore at first, then switch completely to the greedy phase. It has its own sense. At the beginning, we don’t have much intuition so we spend much time for the exploration phase but the rate vanishes as time passes. This is the spirit of UCB and Thompson Sampling. But one thing should be noticed. The exploitation rate is always higher than the exploration one in order to show the consistency of the product.
Which one is better?
Surely, the majority goes with the Bandit approach. There are still some ones who stand for A/B Test. It is still useful when there are not many confusing factors and there are plenty of time for us to run the test. Personally, I think A/B test can play the cold-start for the Bandit (Explore-first scheme)
IV. Contextual Bandits
Contextual Bandits ameliorates MAB by incorporating the context information when making the choice of model (exploration phase). In MAB, the choice is made uniformly. Incorporating state information will reduce the variance of the testing model. It will helps us to raise the efficiency during the exploration step, thus makes the testing more dynamically.