In the most recent post, I talked about some famous clustering algorithms and they work well in reality. However, we the data scientists don’t really like these methods because of one thing: they are deterministic and nothing in data science have that deterministic, especially in unsupervised learning: we don’t have the label so we can’t be so sure about our solution. Hence we are still trying to find some ways to encode the probability in our decision and one way to do this in the problem of clustering is using Mixture Models.
I. What is Mixture Models
Sometimes, we presume that the data we have is generated by a collection of distributions, not only one. In other words, at a moment \(t\), the data \(x_t\) maybe generated by one of the distributions from the pool, and the uncertainty is encoded using the probability.
A well-defined example of Mixture Models is Mixture of Gaussian. The probability densities takes the form of superposition:
\[p(x) = \sum_{k=1}^{K} \pi_k N(x|\mathbf{\mu_k}, \Sigma_k)\] \[\sum_k \pi_k = 1, \pi_k \ge 0\]There are 3 parameters which need solving in order to define the densities: \(\mu_k, \pi_k, \Sigma_k\). We can do that using methods like \(MAP, MLE\) as in the normal Gaussian case.
II. The need of probability encoding in clustering
From my perspective, soft assignment (which provides us the additional information about the probability) is always better than hard assignment(which only cares about the one with highest score). For example, given the list of articles user A has read, we have to find his favorite so that we can give him what he want. Sometimes, the distance from user vector to centroid 2 is just slightly bigger than the smallest one which is the distance to centroid 4. If we play the scheme winner takes it all, it is really inefficient: in this case, maybe user just like two topic equally.
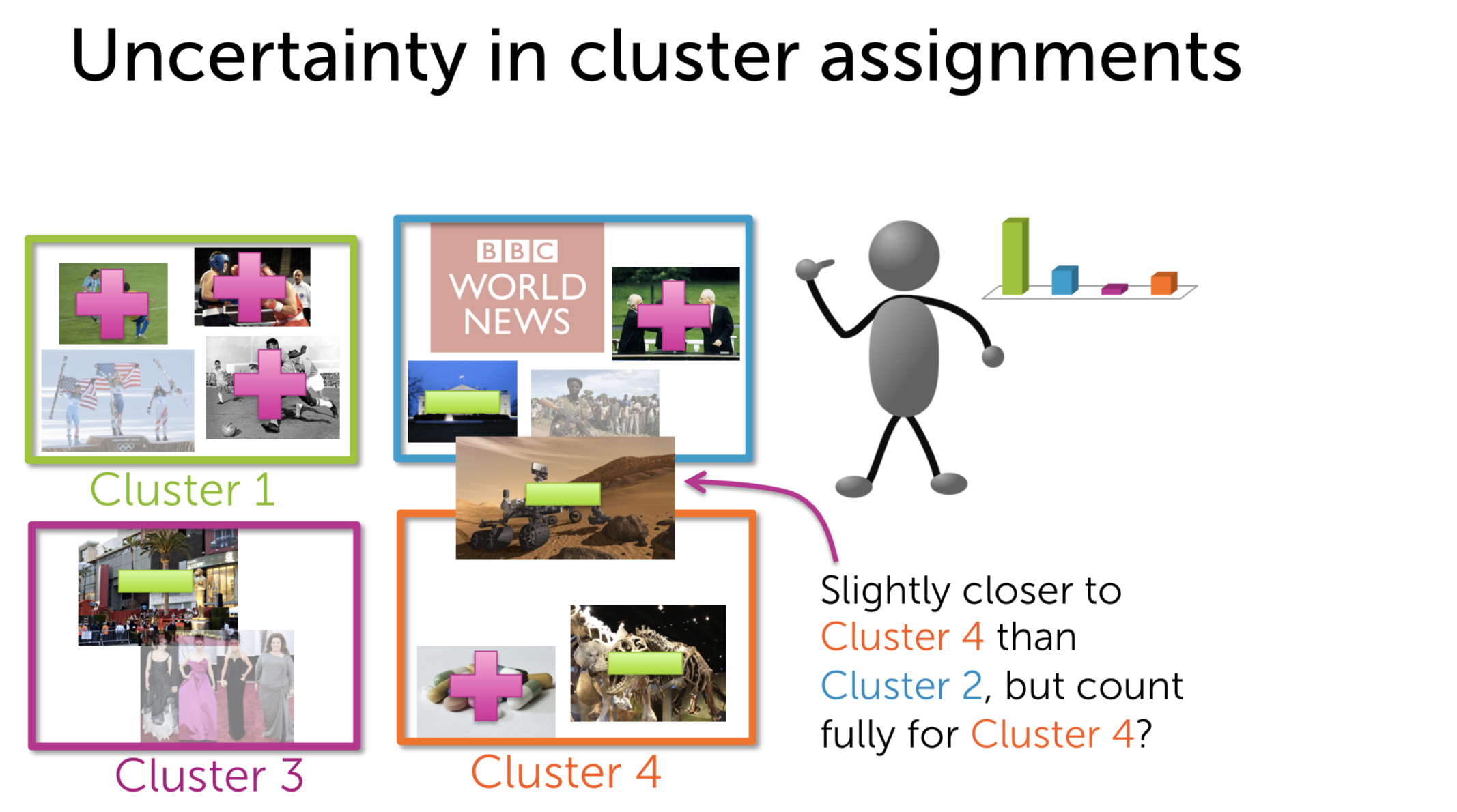
Differently speaking, hard assignment doesn’t welcome the overlap which means a data point belongs to two or more clusters while soft assignment does. It is a big advantage since it gives us more choices to make.
III. Solving the clustering with Mixture of Gaussian
So how to apply this approach to our problems? Suppose we have a set of image with histogram below:

As we can see the distribution from the histogram, our data is a superposition from 3 single Gaussian distributions:
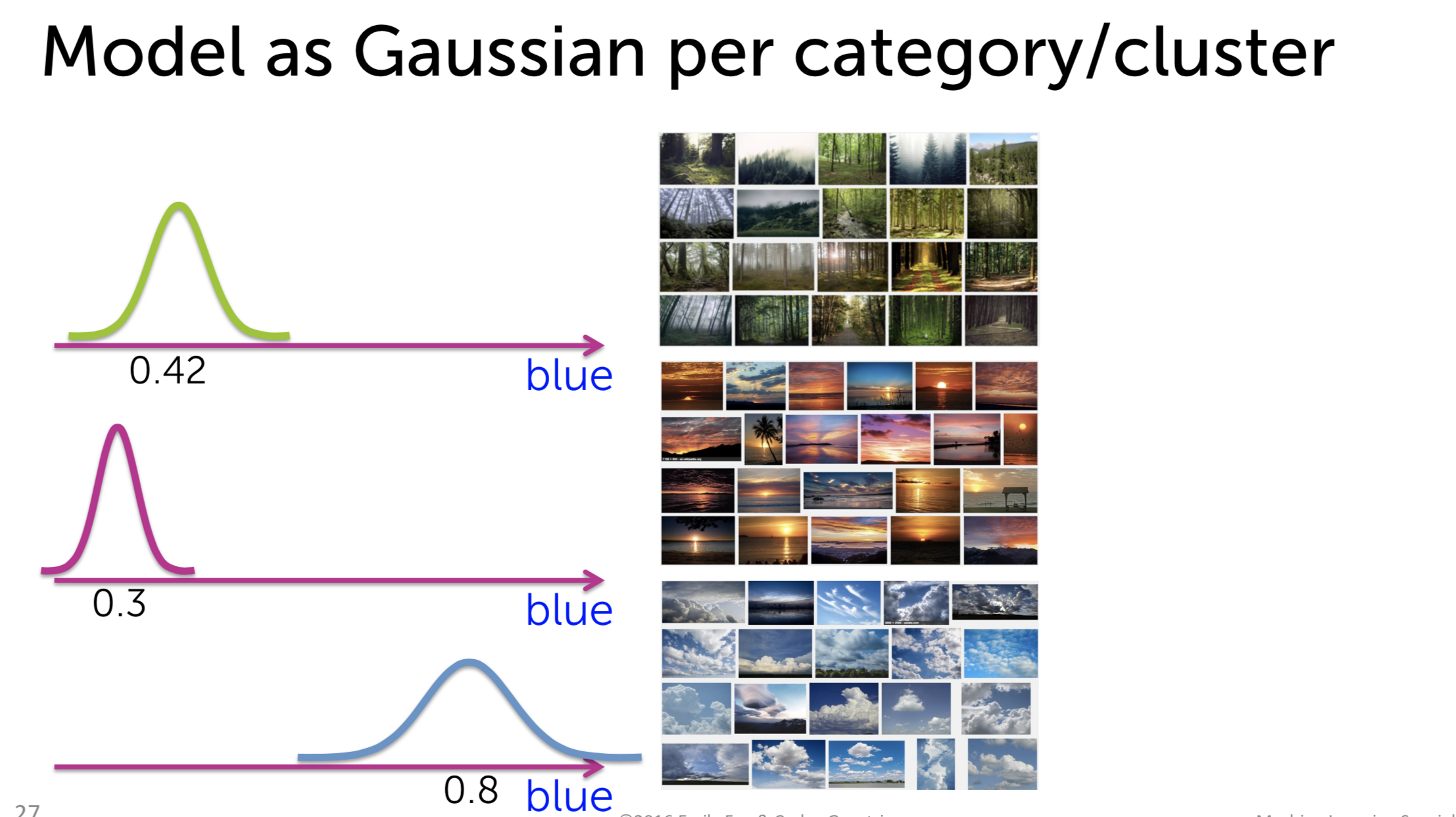
Each Gaussian distribution \(N\) is characterized by its mean \(\mu_k\) and its variance \(\sigma_k\). So what is the role of \(\pi_k\). From the Bayesian view, the weight plays the role of prior probability which describes the proportion of each cluster member in our data-set. It can be considered as our belief of the population of each cluster in the set. Therefore, it has another name as weighted Gaussian
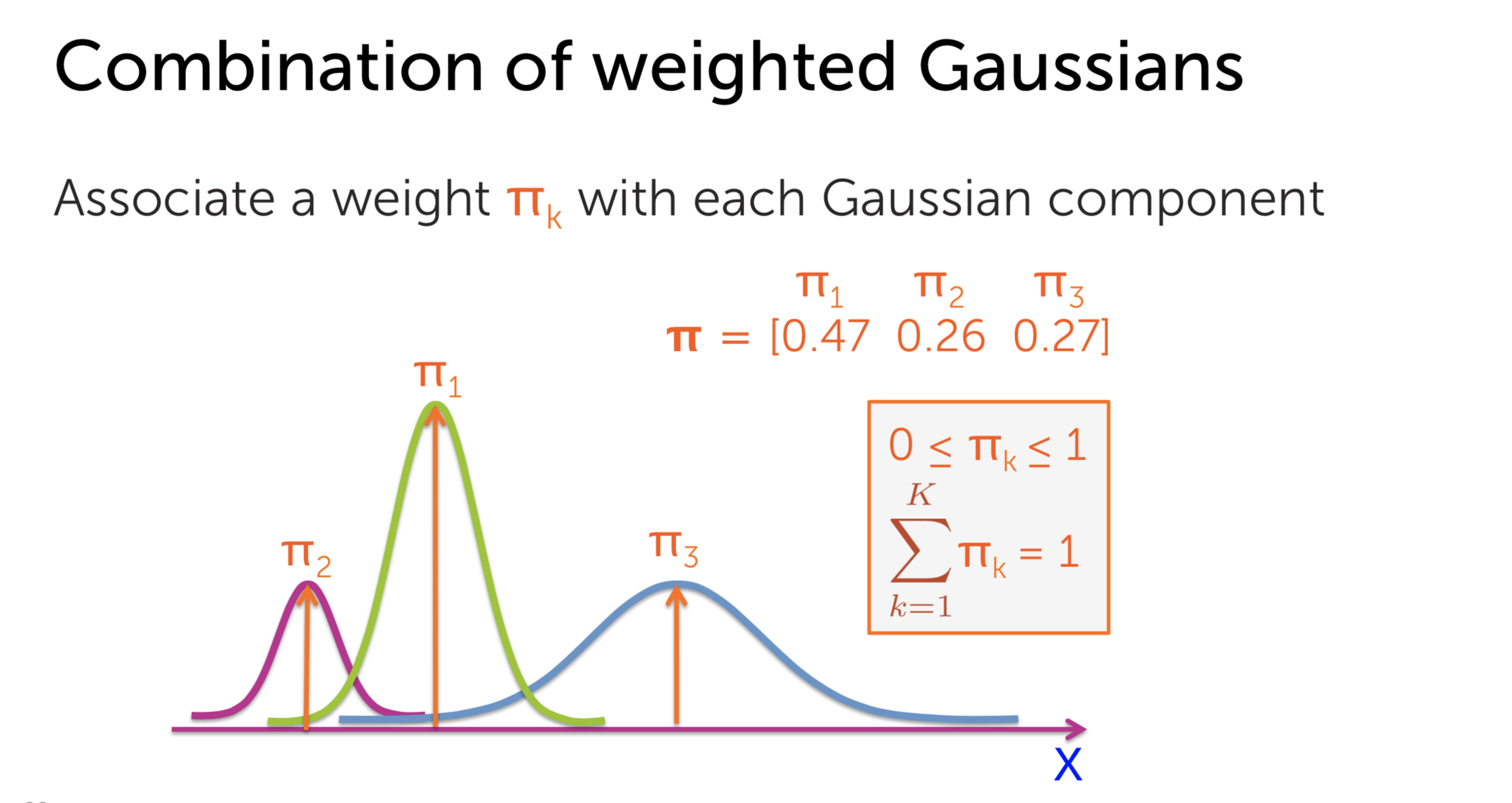
So there are 3 parameters to find. How to compute them? Just like K-Means, we use Expectation Maximization method:
-
Suppose that these parameters are known, we can compute the probabilities that \(x_i\) belongs to cluster \(k\):
\[\hat{r}_{ik} = \frac{\hat{\pi}_k N(x_i | \hat{\mu}_k, \hat{\Sigma}_k)} {\sum_{j=1}^{K}\hat{\pi}_j N(x_i | \hat{\mu}_j, \hat{\Sigma}_j)}\] -
Given the probabilities \(\hat{r}_ik\), maximize the likelihood over parameters
\[\hat{\pi}_k, \hat{\mu}_k, \hat{\Sigma}_k | {x_i, \hat{r}_{ik}}\]